List of invited speakers
| C.Manolescu | |
K.Ono | |
T.Ekholm |
| T.Perutz | |
S.Sarkar | |
J.Rasmussen |
| M.Abouzaid | |
N.Saveliev | |
A.Losev |
| M.Hedden | |
A.Akhmedov | |
A.Stipsicz |
| I.Itenberg | |
O.Ceyhan | |
T.Etgu |
| B.Ozbagci | |
T.Matumoto | |
S. Salur |
| | |
M. Kalafat | |
|
Scientific Committee : D. Auroux, Y. Eliashberg, G. Mikhalkin, R. Stern, S. Akbulut
Organizing Commitee : T. Onder, T. Dereli, S. Kocak, S. Finashin, M. Korkmaz, Y. Ozan
This conference is sponsored by
NSF and IMU
 |
| Mohammed Abouzaid | |
Homological mirror symmetry for toric varieties
I will begin by explaining the statement of the Homological Mirror Symmetry conjecture for Fano toric varieties. I will then show how Mikhalkin's flavour of tropical geometry can be used to prove half of the homological mirror conjecture for all smooth projective toric varieties. |
 |
| Anar Ahmedov | |
Small Exotic 4-Manifolds
In this talk we present new examples of symplectic 4-manifolds with same integral cohomology as S2 x S2. We also discuss the generalization of these examples to (2n-1)S2 x S2 case for n > 1. As an application of these symplectic building blocks, we construct
1) An exotic smooth (symplectic for b2+ = 1) structure on CP2#3(-CP2)3CP2#5(-CP2),
and 3CP2#7(-CP2).
2) An exotic symplectic CP2#5(-CP2).
3) An infinite family of distinct smooth 4-manifolds homeomorphic but not diffemorphic to CP2#3(-CP2), 3CP2#5(-CP2) and 3CP2#7(-CP2).
Part of this is joint work with I. Baykur and D. Park. |
 |
| Denis Auroux | |
Mirror symmetry in the complement of an anticanonical divisor
We discuss a possible approach to the construction of a Landau-Ginzburg mirror for an arbitrary Kahler manifold equipped with an anticanonical divisor. Using a concrete example (CP2) we outline the difficulties that arise in this program. |
 |
| Özgür Ceyhan | |
Chow groups of the moduli spaces of weighted pointed stable curves of genus zero
N-pointed curves with fixed genus can be enriched by assigning a weight to each marked point. The moduli stack Mg,A of weighted pointed stable curves and its variation of with respect to weight data have been studied by Hassett. The moduli space Mg,A is stratified according to the degeneration types of such curves.
In this talk, I will show that the Chow groups of M0,A are generated by the cycles of the strata of M0,A. The additive relations are obtained from the additive relations in Chow groups of M0,n. This result generalizes Kontsevich-Manin's and Losev-Manin's theorems to arbitrary weight data A. |
 |
| Alex Degtyarev | |
Zariski k-plets via dessins d’enfants
We construct exponentially (in the degree) large collections of irreducible plane curves saharing the same set of singularites but not deformation equivalent. All curves constructed have abelian fundamental groups. |
 |
| Tobias Ekholm | |
A surgery exact sequence in linearized contact homology.
We present a long exact sequence which connects the linearized contact homology of a contact manifold with Legendrian sphere, the cyclic contact homology of this Legendrian sphere, and the linearized contact homology of the contact manifold which results after surgery on the Legendrian sphere. The talk reports on joint work with Bourgeois and Eliashberg. |
 |
| Ilia Itenberg | |
Recursive formulas for Welschinger invariants of real Del Pezzo surfaces
(joint work with V. Kharlamov and E. Shustin)
The Welschinger invariants are designed to bound from below the number of real rational curves passing through a given generic real collection of points on a real rational surface. In some cases these invariants can be calculated using Mikhalkin's approach which deals with a corresponding count of tropical curves.
As is known, in certain situations (for example, in the case of generic collections of real points on a toric Del Pezzo surface
equipped with the tautological real structure) there is a logarithmic equivalence between the Welschinger and Gromov-Witten invariants. We consider generic collections of real points on the projective plane blown up at 4 points in general position and, using appropriate tropical Caporaso-Harris type formulas, prove that the logarithmic equivalence of the Welschinger and Gromov-Witten invariants holds in this situation as well. The proof is based on a new version of the correspondence theorem. |
 |
| Matthew Hedden | |
An invariant of knots in a contact manifold
I'll discuss a generalization of the Ozsvath-Szabo concordance invariant which assigns a number to a knot in a three-manifold equipped with a contact structure. Under favorable circumstances, this number provides upper bounds for the Thurston-Bennequin and rotation numbers of Legendrian representatives of the topological knot type in the chosen contact structure. Other applications of this invariant appear to include an interaction with the geometry of complex (resp. J-holomorphic) curves in Stein (resp. symplectic) fillings of the given contact manifold, detection of fibered knots which induce tight contact structures, and invariants of link concordance. |
 |
| Andrei Losev | |
Tropical mirror symmetry and Quantum mechanics
We understand mirror symmetry as correspondence between generating
function for special enumerative problems and deformation of the
generalized (in Barannikov-Kontsevich sense) complex structure on
the dual manifold. For counting curves in projective space (with the
choice of the toric structure) the enumerative problems allows
simple tropical description and can be understood as counting
functions on
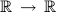 with the piecewise constant integer derivatives. The space of such function
naturally arises in quantum mechanics with the Hilbert space being
with the piecewise constant integer derivatives. The space of such function
naturally arises in quantum mechanics with the Hilbert space being
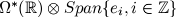 ,
with the second factor being the space of slopes. Mirror is
interpreted as understanding of this factor as the space of
functions on a new circle S1 that together with the original ,
with the second factor being the space of slopes. Mirror is
interpreted as understanding of this factor as the space of
functions on a new circle S1 that together with the original
 forms the mirror manifold. If we denote coordinate on forms the mirror manifold. If we denote coordinate on
 as r, angle on S1 as
U, and degree counting
parameter as q2, then the operator of the dual generalized
complex structure takes the form as r, angle on S1 as
U, and degree counting
parameter as q2, then the operator of the dual generalized
complex structure takes the form
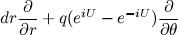 ,
where odd variable θ corresponds to dΦ, where Φ is
an angle variable in the toric structure on the original projective
space. ,
where odd variable θ corresponds to dΦ, where Φ is
an angle variable in the toric structure on the original projective
space.
|
 |
| Ciprian Manolescu | |
The Floer homology of quasi-alternating knots
|
 |
| Takao Matumoto | |
On the smooth unknotting conjecture in dimension four
Any 2-knot is represented by closing a 2-braid. This is an Alexander type theorem. We have also a Markov type theorem due to Kamada. By generalizing this theorem and using the deformation theory of chart diagrams, the smooth unknotting conjecture
in dimension four will be reduced to a special case which will be analyzed separately. |
 |
| Grigory Mikhalkin | |
Floor diagram decompositon
Floor diagrams are tropical-geometric manifestation of a well known technique, used frequently in Symplectic and Algebraic Geometry (known in different settings as stretching the neck or the Caporaso-blams recursion, etc.) Floor diagrams have a simple visiual form and can be used to enumerate tropical, complex and real curves in projective spaces of arbitrary dimension (joint work with E.Brigalle). |
 |
| Kaoru Ono | |
Floer theory for Lagrangian submanifolds and an analog of the flux conjecture for Lagrangian submanifolds
The flux conjecture states that the Hamiltonian diffeomorphism group is closed in the symplectomorphism group with respect to $C^1$-topology. We proved it using Floer theory for symplectomorphisms. We can also consider its analog for Lagrangian submanifolds. Namely, is the quotient space of Lagrangian submanifolds by the Hamiltonian diffeomorphism group Hausdorffor not? It is known to Chekanov that it is not always the case. I would like to discuss the above question in some situations. |
 |
| Tim Perutz | |
A symplectic Gysin sequence and the Floer homology of connected sums
I shall explain that the Gysin sequence for the homology of a sphere-bundle has a counterpart in symplectic Floer homology. Cases of this `symplectic Gysin sequence’ appear as part of a conjectural symplectic model for Seiberg-Witten Floer homology of three-manifolds: they are the analogues of an exact triangle due to Mrowka and Ozsvath describing Floer homology for connected sums. |
 |
| Jacob A Rasmussen | |
Recognizing Berge knots
It is longstanding problem to determine which knots in S^3 admit lens space surgeries. A conjecture due to Berge says that all such knots should have a particularly simple form; the corresponding knot in the lens space should be a 1-bridge braid. Even within this class, however, it is not clear which knots correspond to lens space surgeries in S^3; Berge gives a list of 12 different types which do, but it is unknown if the list is complete. I'll describe how knot Floer homology can be used to reduce this question to a (hopefully tractable) problem in elementary number theory. |
 |
| Sucharit Sarkar | |
An algorithm to compute some Heegaard Floer homologies
We shall review the defintion and some of the properties of Heegaard Floer homology, and find a chain complex which computes one version of it. We shall also try to investigate a few properties of this chain complex. |
 |
| Nikolai Saveliev | |
Dirac Operators on manifolds with periodic ends
This is part of a joint project with Daniel Ruberman aimed at establishing relations between classical invariants of low-dimensional topology and certain invariants arising in gauge theory.
We study Dirac operators on non-compact spin manifolds with periodic ends of dimension at least four and provide a necessary and sufficient condition for them to be Fredholm for a generic end-periodic metric. We use this result to prove that a Cappell-Shaneson invariant provides an obstruction to the existence of metrics of positive scalar curvature on some non orientable 4-manifolds. As an application, we show that some exotic 4-manifolds do not admit a metric of positive scalar curvature in some cases,even if their orientation double covers do).
We further use end-periodic Dirac operators to construct an integral lift of the Rohlin invariant and discuss its possible applications to the study of homology cobordisms. |
 |
| Andras Stipsicz | |
Symplectic rational blow-down and surface singularities
We show that replacing the appropriate neighborhood of symplectic surfaces in a 4-manifold intersecting according to a negative definite matrix by a deformation of the corresponding singularity is a symplectic operation. |
 |
