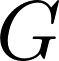
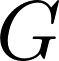
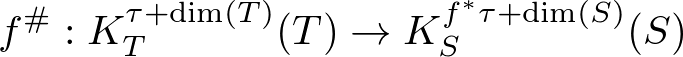
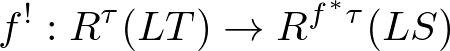
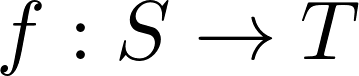
Freed, Hopkins and Teleman constructed an isomorphism (we call it FHT isomorphism) between twisted equivariant K-theory of compact Lie group and the "Verlinde ring" of the loop group of ([FHT1, FHT2, FHT3]). However, naturality of the isomorphism with respect to group homomorphisms has not been verified. We construct induced homomorphisms and for whose tangent map is injective. is a positive central extension of the loop group of , so that FHT isomorphism is a natural transformation between two objects. 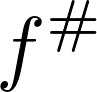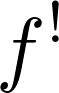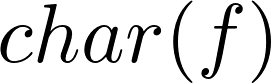In fact, we construct another object char and verify that three objects are naturally isomorphic with respect to , and we introduce. 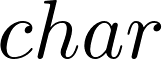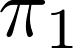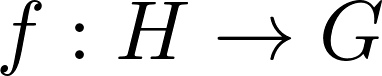Moreover, we extend these constructions for K-theory and to compact connected Lie group with torsion-free and homomorphism satisfying the "decomposable condition", and verify that they are isomorphic. This is a generalization of naturality of verified in [FHT1].